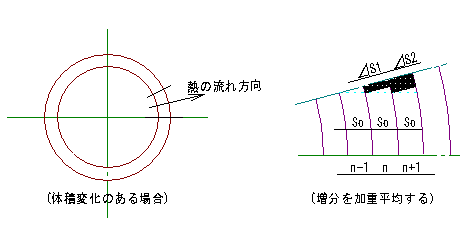
ɽ�̳�¦�β��۲��١ʣ��ˤ�ɤΤ褦�����ꤹ�뤫�������ꡣ
��Ǯ��ã�ˤ�äư�ư����Ǯ�̡���ݦ��ʣ����ݣ����
��Ǯ��Ƴ�ˤ�äư�ư����Ǯ�̡���ݦˣ��ʣ���������
����Ǥ��뤫��
���ݦ��ʣ����ݣ���ˡ�ݦˣ��ʣ��������ˡ����ʣ����ݣ���ˡ�ʦˣ������ˡ��ʣ���������
���ǡ�ˣ��������Ȥ����
���ʣ����ݣ���ˡ��ǡ�ʣ��������ˡ������Ĥ���ϲ��ٸ��ۤǤ��뤫��
�����ޤΤ褦�ˤʤ롣

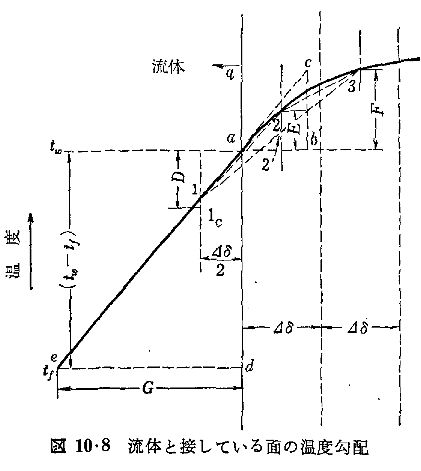
���鵱����������Ǯ��ˡ���𣲣�����
�� �� �桡ή�Τβ���(��ή����)��(��)
�� ���������̤�ɽ�̲��١�(��)
�� �ǡ� ʪ�Τ�Ǯ��ƳΨ��ɽ��Ǯ��ãΨ���ʣ���
�� ���� ������֡ʭ��ӡʣȣ�ˡ˴֤�ʿ�Ѳ����룲���֤ε�Υ�ʣ���
�����������������ġ�ʣ��� �� ���ӡ������������������ʦˡ��ѡ��ãСˡIJ�����ƳΨ�ʣ������ȣ��
�ʺ�ʬˡ�ˤ����Ƥϡ������Ϥ�Ԥ�����ʪ���ͤ��Ѳ�������б��Ǥ��ʤ��ʤ롣��
�ʤ���Ϥ����ޤǤ��ص�Ū����ˡ�Ǥ��롣��
�����ؼ��Ȳ��ټ��Σ���������դ����ꤹ�롣
��������ζŽ���Ǯ���٤˴������롣
���������Ǯ�ѷ������ӡ���������������ѷ���Ǯ�ᣱ���ˣ��졿�ˣ硡����Ǯ�ᣰ��������졿����Ȥ����
����������Ǯ����Ǯ�ᣱ�����������ᣳ������
��Ȥʤ�Τ�
�����������������������������������������������ˤ����夲���롣
���������夲���줿����������ͻ���鲹�٤�Ȥ롣
���������ʣ�������ʤ�С�������������Ȥ��롣��
�������Υ���վ�ǿ����Ϥ�Ԥ������ϸ塢���μ��٤��᤹��
������������Ǯ��Ƴ�ˤ�벹���Ѳ��ϡ��ۤܺƸ��Ǥ���Ȼפ�����Ǯ��ã��ȼ��ɽ�̤β��Ϥˤ��Ρ֤����夲�פ�Ŭ�Ѥ���ȸ����������롣
���ͤäơ������ɽ�̲��٤��ѷ����٤�ã����ޤǤ�Ǯ��ã��β��٤�Ʊ�������֤����夲�פ�Ԥ�������ʲ��ٺ��Ƿ����ˡ��������ٰʲ��ˤʤ�ȡ֤����夲�פ��ˡʤ�Ϥ��̾�β��ٺ��ǡ˷�����ɬ�פ����롣
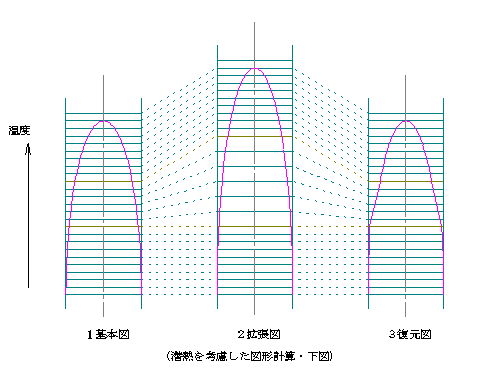
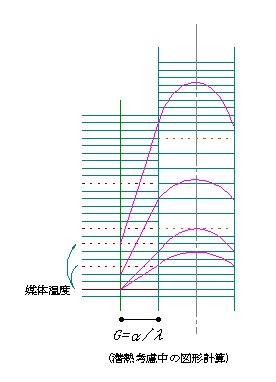
�����������Ϥ�ʿ�̤����оݤˤʤ�ʤ������ߤ�������������Ǯ��ߥ졼�Ȥ���Ȥ��������֤β��٤�ʿ�Ѥ���Ȥ������Ѥ��礭������������������������ݤ���ʿ�Ѳ����뤳�Ȥ�¿�������Ǥ��롣
�����ԡʣ�ˡ�ʣԡʣ�ݣ��ˡܣԡʣ�ܣ��ˡˡ������λ���
���������ԡʣ�ݣ��ˤ����Ѥ� �ԡʣ�ܣ��ˤ����Ѥ�ꡢ�����礭�������
�����ԡʣ�ˡ�ʣ����������ԡʣ�ݣ��ˡܣԡʣ�ܣ��ˡˡ�����
���������Ȥ��뤳�Ȥǡ�¿�������Ǥ��롣